Quantitative Data

Objectives

At the end of the lesson, you should be able to identify Systeme International (SI) units of measurement, represent quantitative data in correct significant figures, and convert very large or very small numbers to scientific notation

Some quantities are easy to measure. The length of a pencil is easy to get with a ruler. However, some quantities are either very large like Earth’s circumference, or very small like the mass of a grain of sand. How do these numbers help scientists draw conclusions?

Measurement

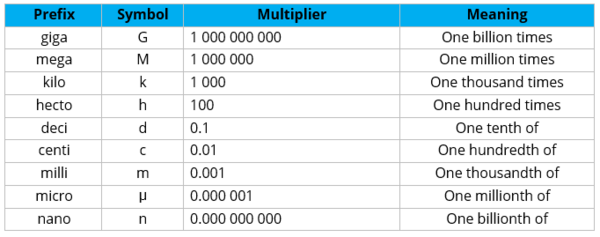
Measurement is the process of finding out how many measuring units are contained in an event or object based on a certain set of standards. Early on, the metric system is the agreed system of measurement created in France. In the metric system, each type of measurement has a basic unit of measure. Conversions can be done easily by multiplying by factors of 10 and adding prefixes to the units of measurement.

For example, when a measurement reads one kilometer, this is the same as saying one thousand meters. One nanometer, on the other hand, is the same as one billionth of a meter.

However, the metric system however was not adopted in the US. The US English system of measurement is derived from day to day activities using body parts and common objects. For example, the distance was measured in the foot while volume was measured in cups. This led to discrepancies in the measurement and confusion when comparing the metric and the English units.

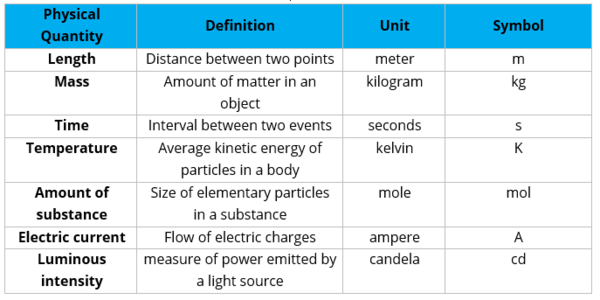
In order to avoid confusion, the Systeme International d’Unites or the International System of Units (SI unit) was agreed by many scientific agencies.

There are seven fundamental quantities in the SI unit. The seven fundamental quantities and their basic units are as shown below.

Units of measurements that are derived from fundamental units are called derived units.

Significant Figures

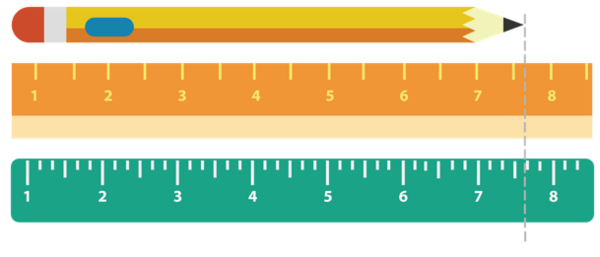
Measurements depend on the tool used. For example, a pencil may be measured using two different rulers as seen in the figure below.

Using the first ruler, you are certain that the pencil is more than 7 cm, but you are not sure however if it is 7.5 7.6, or 7.7 cm. The first digit 7 is certain but the second digit is “a guess.” The length of the pencil is then reported as 7.5 cm wherein you are sure of the digit 7, while 5 is a guess.

Using the second ruler, you are sure that the pencil is more than 7.6 cm. You can guess that it can be around 7.69 cm. You can record the length of the pencil therefore as 7.69 cm wherein you are sure of the digits 7 and 6, while 9 is a guess.

In recording measurements, you should always retain only one uncertain digit. All digits that you are sure of and the one uncertain digit are called significant figures.

How do you determine significant figures when presented with a quantitative data?

If the quantitative data is obtained from measurements, there are some rules that you need to follow to determine the number of significant figures when given a quantitative data

1. All nonzero digits are significant
1. Zeroes between nonzero digits are significant.
1. In a decimal number less than 1, zeroes before the first nonzero digit (leading zeroes) are not significant.
1. Zeroes after the last nonzero digit (trailing zeroes) in a number with a decimal are significant.
1. Zeroes after the last nonzero digit (trailing zeroes) without a decimal point are not significant.

Scientific Notation

Some measurements are very large like the speed of light very small like the average thickness of hair. It will take up too much space and time to write all these numbers.

A more convenient way of writing these numbers is to rewrite them in scientific notation. The scientific notation is a systematic way of writing very large or very small numbers.

A scientific notation is written as

C.MM x 10e

where C is the characteristics digit, M is the mantissa digit, and e is the number of times the characteristic and mantissa digits is multiplied by 10.

The characteristic and mantissa digits comprise the coefficient. The coefficient is any decimal number greater than or equal to 1 but less than 10.

Tips

• In dealing with significant figures, always be mindful of the zeroes.
• To easily determine if a zero is significant or not, draw a line following the direction of the arrows below for whole number and decimal numbers until you reach the first non-zero digit. Count the remaining digits to identify the number of significant figures.
• In writing scientific notation, try drawing arrows to help you count how many places the decimal point must be moved. Numbers that are greater than 1 have a positive exponent while numbers that are less than 1 have a negative exponent.

Key Points

• Measurement is the process of finding out how many measuring units are contained in an event or object based on a certain set of standards.
• The seven fundamental quantities are length, mass, time, temperature, amount of substance, electric current, and luminous intensity.
• All digits that you are sure of and the one uncertain digit are called significant figures.
• A more convenient way of writing these numbers is to rewrite them in scientific notation.